| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 코딩테스트
- codingtest
- 머신러닝
- 파이썬
- wordcloud
- 백준
- selenium
- Tensor
- Python
- Overfitting
- 분산 시스템
- 코테
- TF-IDF
- 데이터
- SGD
- 웹크롤링
- pytorch
- coursera
- 시각화
- 추천 시스템
- 알고리즘
- 데이터 엔지니어링
- 협업 필터링
- 웹스크래핑
- 추천시스템
- Cosine-similarity
- recommendation system
- 프로그래머스
- 부스트캠프
- 딥러닝
- Today
- Total
개발자식
[머신러닝] 선형 회귀 (Linear Regression) 본문
머신러닝의 가장 큰 목적은 실제 데이터를 바탕으로 모델을 생성해서 다른 입력 값을 넣었을 때 발생할 아웃풋을 예측하는 데 있다.
이때 찾아낼 수 있는 가장 직관적이고 간단한 모델은 선이다. 이러한 선을 찾고 분석하는 방법을 선형 회귀 분석이라고 부른다.
선형 회귀 (Linear Regression)
: 종속 변수 y와 한 개 이상의 독립 변수 (=설명 변수) x 사이의 선형 상관 관계를 모델링하는 회귀분석 기법
- 정답이 있는 데이터의 추세를 잘 설명하는 선형 함수를 찾아 x에 대한 y를 예측
ex) 키가 클수록 몸무게가 무겁다, 집의 평수가 클수록 집의 매매 가격은 비싸다
단순 회귀분석 (Simple Regression Analysis)

: 1개의 독립변수 x가 1개의 종속변수 y에 영향을 미칠 때
- 독립 변수 x에 곱해지는 w값을 가중치(weight), 상수항에 해당하는 b를 편향(bias)라고 부른다.
- 그래프의 형태는 직선으로 나타난다.
다중 회귀분석 (Multivariate Regression Analysis)
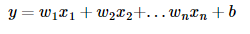
: 2개 이상의 독립변수 x가 1개의 종속변수 y에 영향을 미칠 때
- 2개의 독립 변수면 그래프는 평면으로 나타난다.
그래서 회귀 분석의 목표는?
-> 회귀분석은 가장 적합한 세타(w, b) 들의 set을 찾는 것이 목표이다.
가설 세우기
- 아래와 같이 어떤 학생의 공부 시간에 따른 점수 데이터가 있다고 할 때 이 학생의 6시간, 7시간, 8시간을 공부하였을 때의 성적을 예측해보고 싶다면 x와 y의 관계를 유추하기 위해 수학적으로 식을 세워 보는데 머신러닝에서 이러한 식을 가설이라고 한다.


- 위 사진에서는 같이 w와 b의 값에 따라 다양하게 그려지는 직선의 모습을 보여준다. 선형 회귀는 주어진 데이터로부터 y와 x의 관계를 가장 잘 나타내는 직선을 그리는 일이다.
- 가장 적합한 직선을 찾고 x가 6시간, 7시간, 8시간 일 때에 대해서도 계속해서 직선을 이어 그린 다면 각각의 시간에 대한 예상 점수는 각각의 y 값을 확인하면 된다.
가장 적합한 직선이 무엇일까?
: 변수 x와 y의 관계를 가장 잘 나타낸다는 것은 x,y의 좌표로 나타낸 점들 에 가장 가까이 있는 직선을 찾는 것
-> 즉 모든 점들과의 거리의 합이 최소가 되는 직선을 찾는 것이다.

-> 분홍색 선이 예측한 값과 실제값의 차이인 error(오차, 잔차)를 나타내는데 이 격차가 좁을수록 정확도가 높다.
* 격차가 음의 값인지 양의 값인지 중요하지 않고 절대값이 중요하다. -> 제곱을 이용
오차가 적은 직선을 어떻게 구할까?
-> H(x)= Wx+b라고 가설을 세웠을 때 H(xi)값(예측 값)과 yi(실제 값)값의 차이의 제곱 값의 평균이 가장 작은 W와 b를 구해야 한다.

여기서 Cost Function (비용 함수)은 예측 값과 실제 값의 차이를 기반으로 모델의 성능(정확도)을 판단(평가) 하기 위한 함수이다.
- cost function == loss function, error function, objective function
그래서 오차가 적은 직선을 구하기 위해서 H(x), Cost function이 필요하다.
Cost Function은 어떻게 생겼는데?
bias term을 삭제하고, H(x)=Wx라고 생각하면 cost(W)는 아래 사진과 같다.

- 2차원 함수의 형태를 띈다.
그렇다면 cost function에서 가장 작은 cost를 어떻게 구하면 좋을까??
-> '경사하강법'을 활용한다.
예를 들어, 안개가 낀 높은 산에서 가장 낮은 곳으로 이동해야 할 때 어떻게 내려가야 할까?
현재 위치에서 모든 방향으로 산을 더듬어가며 산의 높이가 가장 낮아지는 방향으로 한 발씩 내딛어 최종적으로 산을 내려가다보면 가장 낮은 곳으로 이동할 수 있을 것이다. 이러한 방법이 '경사 하강법'이다.
경사하강법
: 비용(cost, 오차의 제곱(MSE))의 값을 줄이기 위해 반복적으로 기울기를 계산하며 변수(가중치 w, 편향 b)의 값을 변경해나가는 과정이다.
목표로 한 값(기울기가 0에 가까운 값)에 가까워질 때까지 계속해서 업데이트(수정)해주면서 최적의 세타(w, b)를 찾는다.

-> 위 그래프의 접선의 기울기가 0인 지점을 기준으로 왼쪽에서 미분했을 때와 오른쪽에서 미분했을 때 서로 다른 방향의 기울기를 얻을 수 있다.
이를 이용하면 직선의 기울기를 어느 방향으로 수정해야 비용이 감소하는지 알 수 있다.
즉, 미분값이 0에 가깝도록 이동한다. 미분했을 때 양수 값이면 작아져야 하니까 왼쪽으로 이동하고 미분했을 때 음수 값이면 커져야 하니까 오른쪽으로 이동한다.
기울기가 0에 가까워지는 값을 찾기 위해 특정 구간을 이동하는 하이퍼 파라미터인 learning rate 이용한다. -> 보폭 개념
Learning rate
- learning rate 값이 작을 때
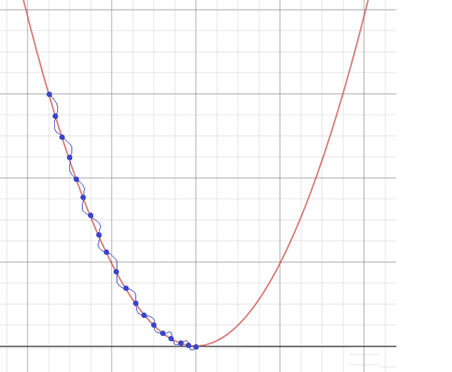
-> 학습을 많이 해야 한다는 단점
- learning rate 값이 클 때

-> 최소의 cost 지점을 벗어나 발산해버릴 수 있다. (오버 슈팅)
learning rate를 상황에 따라 적절하게 설정해야 한다.
learning rate는 초반에 많은 폭으로 변화를 하고 가까워질수록 좁게 뛴다. 이것은 곡선의 특성상 cost가 0인 지점으로 이동할수록 그래프가 완만해지기 때문이다.
-> 아래 사진과 같이 점점 작은 폭으로 뛸 때, 합리적인 직선을 거의 찾았다고 생각하면 된다.

경사 하강법 공식
: 최적의 세타 값을 찾기 위해 세타에 대해서 편미분 해준 것에 학습률을 곱한 것을 초기 설정된 세타 값에서 빼주는 방법을 반복한다.

- Gradient : 모든 변수의 편미분을 벡터로 정리한 것 ( =함수의 기울기, 경사)
- 편미분 : 변수가 2개 이상인 함수를 미분할 때 미분 대상 변수 외에 나머지 변수를 상수처럼 고정시켜 미분하는 것
- 미분 값이 마이너스라면 플러스 방향으로 이동하고 미분값이 플러스라면 마이너스 방향으로 이동한다.
이렇게 최적의 세타를 구하는 것이 경사 하강법의 목표이고 경사 하강법을 이용하는 이유는 최소의 비용을 찾기 위해서이고 이 세타를 이용하여 가장 적합한(최소의 비용을 갖는) 선형 회귀 모델을 만든다고 보면 될 것 같다.
회귀 모형 검증
- 모델의 성능을 검증, 평가하는 것은 지도 학습인 경우에만 사용된다. 지도 학습인 경우 정답이 주어져있기 때문에 내가 만든 모형이 잘 만들어진 것인지 아닌지 판단할 수 있다.
- 회귀 모델을 평가하는 대표적인 지표는 MSE(Mean Squared Error)와 R2(R-squre)이다.
- MSE : 실제값과 예측값의 차이를 제곱한 뒤, 평균을 내는 것이다. 이름에서도 알 수 있듯 오차이기 때문에 MSE값은 작을수록 좋다. 회귀 분석을 위한 대표적인 비용 함수이다.
- R-squre(결정계수) : 전체 데이터를 회귀 모형이 얼마나 잘 설명하고 있는지를 보여주는 지표로서, 회귀선의 정확도를 평가하므로 이 값이 1에 가까울수록 정확도가 높다.
우리가 구하고자하는 현실 값과 가장 유사한 회귀 모형을 만드는 방법을 알아봤다.
독립 변수가 1개이면 단순 회귀분석식, 독립 변수가 2개 이상이면 다중 회귀분석식으로 가설을 세운다.
그리고 예측값과 현실값의 차이의 제곱 합의 평균을 계산하는 cost function에서 가장 작은 값(->에러가 가장 작음)을 구한다. 이때 파라미터가 우리가 찾는 회귀 모형이다. 그리고 가장 작은 값을 구하는 방식은 경사하강법을 이용한다. 경사하강법은 현재 위치에서 미분하여 함수의 최솟값을 찾아가는 방식이다. 사실은 기울기가 가리키는 곳에 최솟값이 있을지 보장할 순 없지만 그 방향으로 가면 함수의 값을 줄일 수 있으므로 찾는 방법이다.
하지만 경사 하강법도 문제점이 있다. learning rate를 잘 설정해야하고 local minimum에 빠질 수 있다.
local minimum에 대해 다음 포스팅에서..
'AI > Machine Learning' 카테고리의 다른 글
| [머신러닝] 감성분류 모델링, XGBoost (1) | 2022.05.20 |
|---|---|
| [머신러닝] Confusion matrix_분류 모델 성능 평가 지표 (0) | 2022.04.27 |
| [머신러닝] ROC Curve & AUC (0) | 2022.04.27 |
| [머신러닝] 로지스틱 회귀 (Logistic Regression) (0) | 2022.04.24 |
| [머신러닝] 교차 검증(CV_K-fold) (0) | 2022.04.24 |




